Geometria analítica
Segundo o site http://pt.wikipedia.org/wiki/Geometria_anal%C3%ADtica em matemática, a expressão geometria analítica possui dois significados distintos. O significado moderno e avançado se refere à geometria das variedades analíticas.
A geometria analítica, também chamada geometria de coordenadas e de geometria cartesiana, é o estudo da geometria por meio de um sistema de coordenadas e dos princípios da álgebra e da análise. Ela contrasta com a abordagem sintética da geometria euclidiana, em que certas noções geométricas são consideradas primitivas, e é utilizado o raciocínio dedutivo a partir de axiomas e teoremas para obter proposições verdadeiras. A geometria analítica é muito utilizada na física e na engenharia, e é o fundamento das áreas mais modernas da geometria, incluindo geometria algébrica, diferencial, discreta e computacional.
A introdução da geometria analítica constituiu o início da matemática moderna. A geometria analítica é atribuída tradicionalmente a René Descartes, que fez um progresso significante em seus métodos em um ensaio chamado Geometria, que foi um dos anexos publicados no seu Discurso do Método, em 1637.
René Descartes deve ser considerado um gênio da Matemática, pois relacionou a Álgebra com a Geometria, o resultado desse estudo foi à criação do Plano Cartesiano. Essa fusão resultou na Geometria Analítica. Descartes obteve grande destaque nos ramos da Filosofia e da Física, sendo considerado peça fundamental na Revolução Científica, por várias vezes foi chamado de pai da Matemática moderna. Ele defendia que a Matemática dispunha de conhecimentos técnicos para a evolução de qualquer área de conhecimento.
Além do Cálculo e da Geometria Analítica, os estudos de Descartes permitiram o desenvolvimento da Cartografia, ciência responsável pelos aspectos matemáticos ligados à construção de mapas.
Podemos relacionar os seguintes tópicos ao estudo da geometria analítica:
Estudo Analítico do Ponto
Plano Cartesiano
Distância entre dois pontos
Ponto médio de um segmento
Condição de alinhamento de três pontos
Estudo da Reta
Equação geral e reduzida da reta
Intersecção entre retas
Paralelismo
Perpendicularidade
Ângulos entre retas
Distância entre ponto e reta
Estudo da Circunferência
Equação geral e reduzida da circunferência
Posições relativas entre ponto e circunferência
Posições relativas entre reta e circunferência
Problemas relacionados à tangência
Estudo das Cônicas
Elipse
Hipérbole
Parábola Intersecção entre cônicas
Retas tangentes a uma cônica
Estudo Analítico do Ponto
Plano Cartesiano
Distância entre dois pontos
Ponto médio de um segmento
Condição de alinhamento de três pontos
Estudo da Reta
Equação geral e reduzida da reta
Intersecção entre retas
Paralelismo
Perpendicularidade
Ângulos entre retas
Distância entre ponto e reta
Estudo da Circunferência
Equação geral e reduzida da circunferência
Posições relativas entre ponto e circunferência
Posições relativas entre reta e circunferência
Problemas relacionados à tangência
Estudo das Cônicas
Elipse
Hipérbole
Parábola Intersecção entre cônicas
Retas tangentes a uma cônica
Encontramos bons vídeos sobre geometria analítica no site www.youtube.com/watch?v=L7g3Jt9BpGU do prof. Jairo que ensina aos seus alunos a desenvolver os cálculos de geometria analítica.
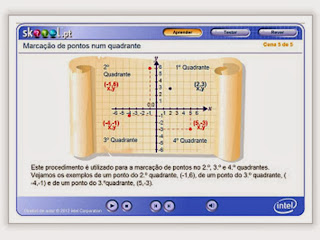
Podemos encontra jogos e Conceitos sobre Geometria Analítica

Grupo: Celso Edir Kautzmann, Marcos Alair Berghahn, Ricardo Ribas.